注意力模型

^ _ ^

Motivation

Seq2Seq

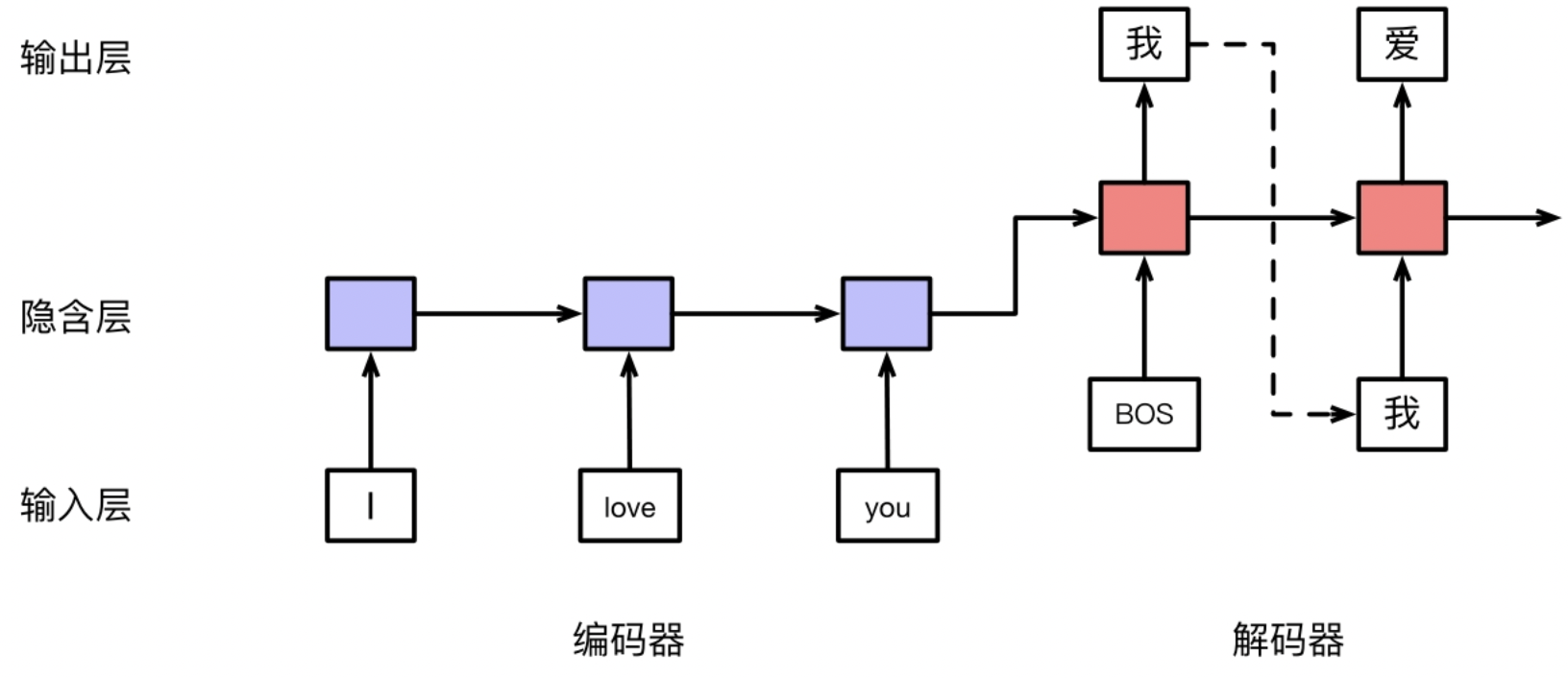
Above figure show an application which uses Seq2Seq Model to realize Machine Translation. Seq2Seq model is composed of 2 parts, respectivly Encoder and Decoder :

1. origin sequence encodes to one coding.
2. Then decode the coding to the target sequence.

RNN for Seq2Seq

Besides Classfication and Sequence Labeling, RNN can also solved Reading Comprehension and Text Generation, which is corresponded to Seq2Seq Model.
Seq2Seq based on RNN:

1. Use RNN to encode origin sequence.
2. Use the last hidden state of encoder RNN as the input, invoking decoder RNN to generate target sequence word by word.

There is a basic hypothesis for Seq2Seq based on RNN: The last hidden state in the encoder RNN contains all the information of the origin sequence.
Obviously, the hypothesis is unreasonable, especially for long origin sequence.

To solve the problem, someone proposed Attention Model.

Attention Mechanism

The core idea of Attention Machinism: When generating a new target word, not noly considering previous time state and already generated word, but also considering which words in the origin sequence is more relevant to the current word need to generate. It guides us put more attention to the words in the source sequence which is more relevant to the current word.

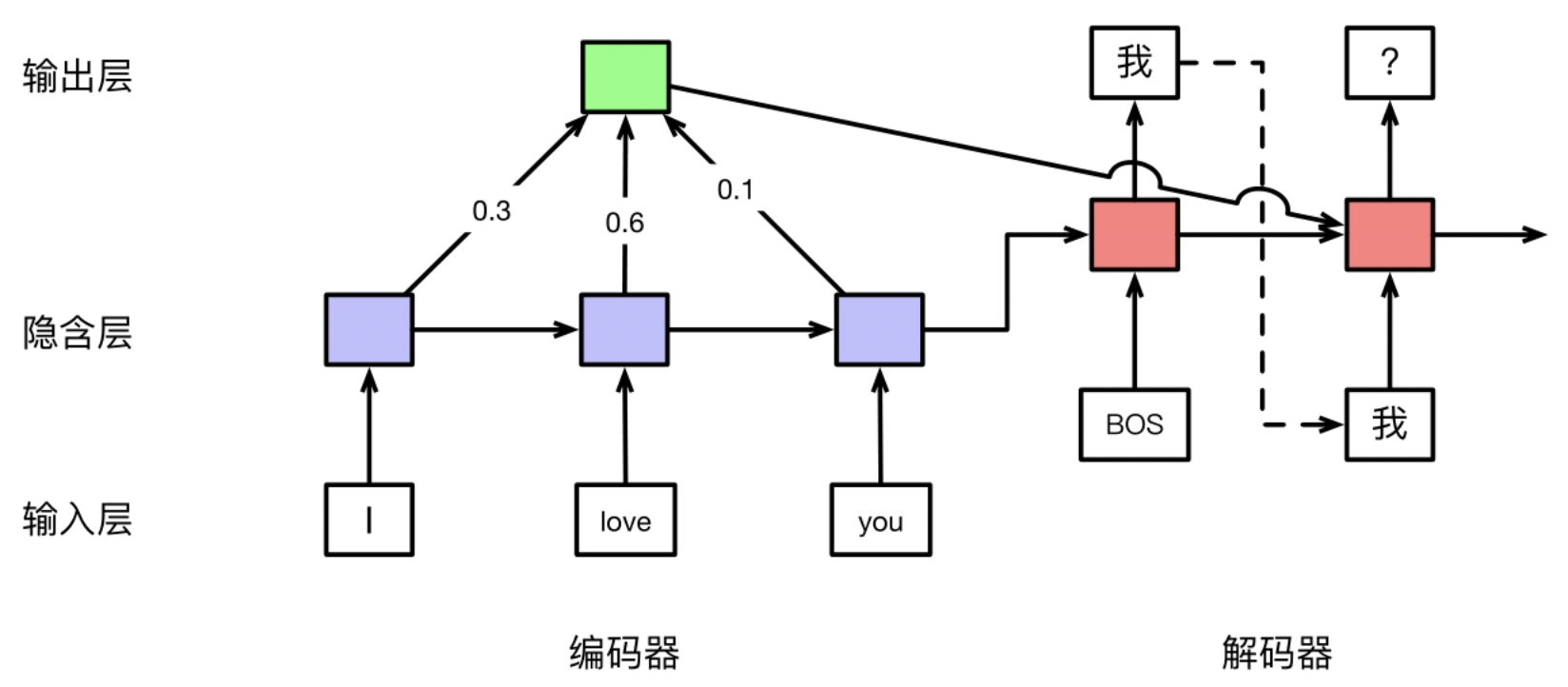
Mathmatically,

$$ \begin{matrix} \hat{\alpha_s} = attn(h_s, h_{t-1}) \\ \alpha_s = Softmax(\hat{\alpha})_s \end{matrix} $$

• $h_s$: the state of time $s$ in the source sequence.
• $h_{t-1}$: the state of previous time in the target sequence.
• $attn$: attention calculation formula.
• $\hat{\alpha} = [\hat{\alpha}_1, \hat{\alpha}_2, \cdots, \hat{\alpha}_L]$, where $L$ is the length of source sequence.
• $Softmax$: Normalize attention score.

Attention Calculation Formula

Self Attention

The core idea of Self-Attention: Observe its companion, then know its meaning. In other word, the state of one point in the sequence can be calculated by the correlation(attention) between the state at this time and the state at other times.

Specifically,

• inputs can be represented by one combination of n vectors: $x_1, x_2, \cdots, x_n$.
• outputs can be represented by one combination of n new vectors: $y_1, y_2, \cdots, y_n$.
• The calculation formulate of $y_i$: $y_i = \sum_{j=1}^n a_{ij}x_{j}$
  • $a_{ij}$ is the attention weight(after softmax normalize) between $x_i$ and $x_j$.

Through the self-attention machanism, the relationship between two distant moments can be directly calculated.

Transformer

Motivation

There are some problems needed to fix of Self-Attention Model.

• There is no consideration about position information when calculating self attention.
• input vector $x_i$ is responsible for 3 roles, which caused it hard to learn:
  • one of two vectors when calculating attention weight.
  • the weighted vector(被加权的向量)
• only considering relationship of 2 units, but not be able to represent multiple relationship between multiple input units.
• the results of self-attention are mutually exclusive, and multiple inputs can not be concerned at the same time.

Transformer can solve these problems.

Transformer Mechanism

Just as its name implies, Transformer transfer a vector sequence into another vector sequence.

Importing Position Information

We need to import position information for every input vector. There are 2 ways to import position information:

1. Position Embeddings(位置嵌入): Like word embedding, use a continues, lower dimension, dense vector to represent position information.
2. Position Encodings(位置编码): Use function to map a position index(integer) to a vector.
   

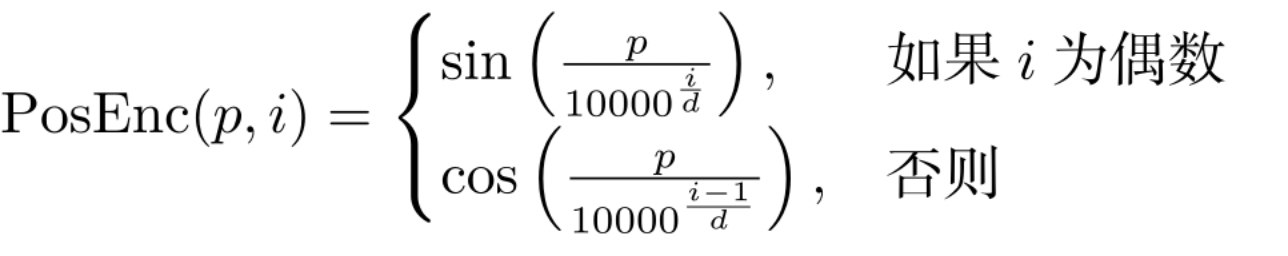
• $p$ indicates the position index.
• $0 \leq i \lt d$ is the index of encoding vector. The dimension of the vector is $d$.

Whatever use Position Embeddings or Position Encodings, after we get a position vector, we add it into the word vecotr, then the result is the final input vector. In result of importing position information, same word in different position will be represented by different vector.

Importing Role Information

In the original Attention Machenism, a input vector acts 3 roles: Query, Key, Value. The better way is represent different role with different vector.

The core idea of import role information is Different Linear Transforamtion for Input Vector. By the way, a linear transformation can be represented by a Parameter Matrix.

Input vector $x_i$ will map to 3 new vectors by 3 different parameter matrixes:

• $q_i = W^q x_i$
• $k_i = W^k x_i$
• $v_i = W^v x_i$

New Calculation Formulation

$$ \begin{matrix} y_i = \sum_{j=1}^n = \alpha_{ij}v_j \\ \alpha_{ij} = Softmax(\hat{\alpha}_i)_j, \hat{\alpha}_{i} = [\hat{\alpha}_{i1},\hat{\alpha}_{i2},\cdots,\hat{\alpha}_{iL}] \\ \hat{\alpha}_{ij} = attn(q_i, k_j) \end{matrix} $$

Multiple Layer Attention

In the original Attention Machenism, it only considers the relationship between 2 input sequence units. But in practical applications, it is often necessary to consider the relationship between many sequence units. If we consturct higher order relationship, it will result higher model complexity.

To solve this demands, someone proposed Message Propagation, which can realized by stacking multiple layer self-attention model. Normally, attention calculation use linear function. So the result of stacking them will also be linear. In order to enhance the presentation ability of model, we can add non-linear MLP behind every attention layer.

In addition, in order to benefit the process of model learning, we can also use some techniques, such as Layer Normalization, Residual Connections.

All the layers stacked to construct a Transformer Block.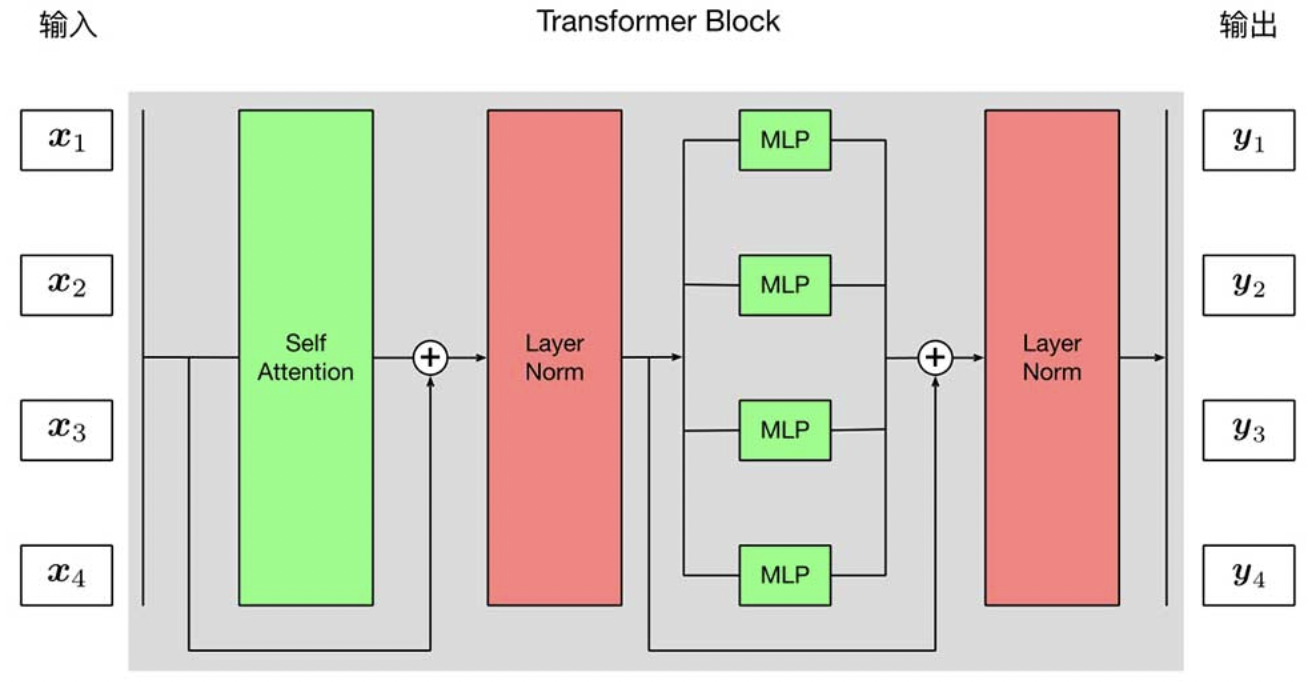

Multi-Head Machenism

Since the result of self-attention need to be normalized, even if an input is related to multiple other inputs, they can not be given a large attention weight at the same time. In the other word, the results of self-attention is exclusive.

To solve this problem, the core idea is:

• Set multiple groups of mapping matrixes.
• Concating all the outputs of every results after those mapping.
• Through a linear mappping, map the concated output to a vector of dimension d.

In other view, Multi-Head Attention Machenism is equal to Ensemble of multiple Self-Attention Model, like different kernels in the CNN.

Seq2Seq based on Transformer

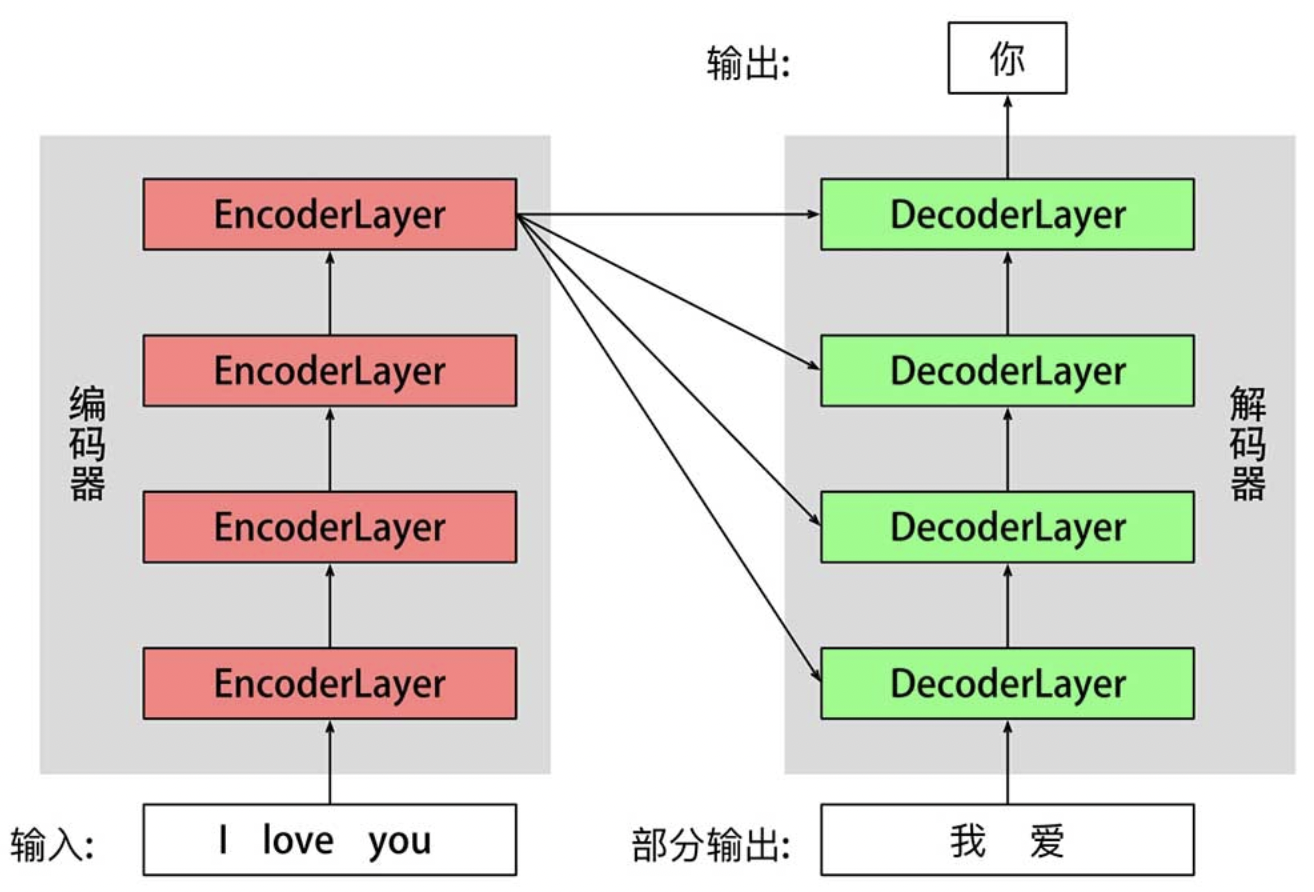
Pros & Cons

Advantages:

• Good at processing Long Distant Relationship between words.
• Can be parallel, which will result rapider training speed.

Disadvantages:

• Too much parameters.
  • Bert: 12 layers transformer block, 1.1 million parameters.
  • Bert-large: 12 layers transformer block, 3.4 million parameters.

Code

import torch.nn as nn

# input_dim: 4; head_num: 2
encoder_layer = nn.TransformerEncoderLayer(d_model=4, nhead=2)
# input size: [seq_len, batch_size, input_dim]
# output size: [seq_len, batch_size, input_dim]
src = torch.rand(2, 3, 4)
out = encoder_layer(src)

# stacking encoder layer
transformer_encoder = nn.TransformerEncoder(encoder_layer, num_layers=6)
output = transformer_encoder(src)
memory = trandormer_encoder(src)

# decoder
decoder_layer = nn.TransformerDecoderLayer(d_model=4, nhead=2)
transformer_decoder = nn.TransformerDecoder(decoder_layer, num_layers=6)
out_part = torch.rand(2, 3, 4)
out = transformer_decoder(output_part, memory)