循环神经网络

^ _ ^

RNN Structure

Recurrent Neural Netword refers to the hidden layer output of the network as its own input.

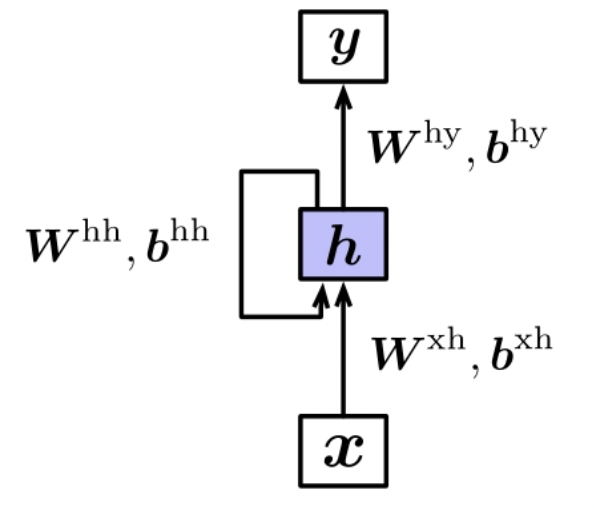
(1) $W^{xh}, b^{xh}$: input layer –> hidden layer
(2) $W^{hh}, b^{hh}$: hidden layer –> hidden layer
(3) $W^{hy}, b^{hy}$: hidden layer –> output layer

When the RNN process a sequence input, it need to expand the network according to input time. Then:

• Every input of sequence will align to the different time unit.
• And every output of the previous time will also be the input of this time unit.

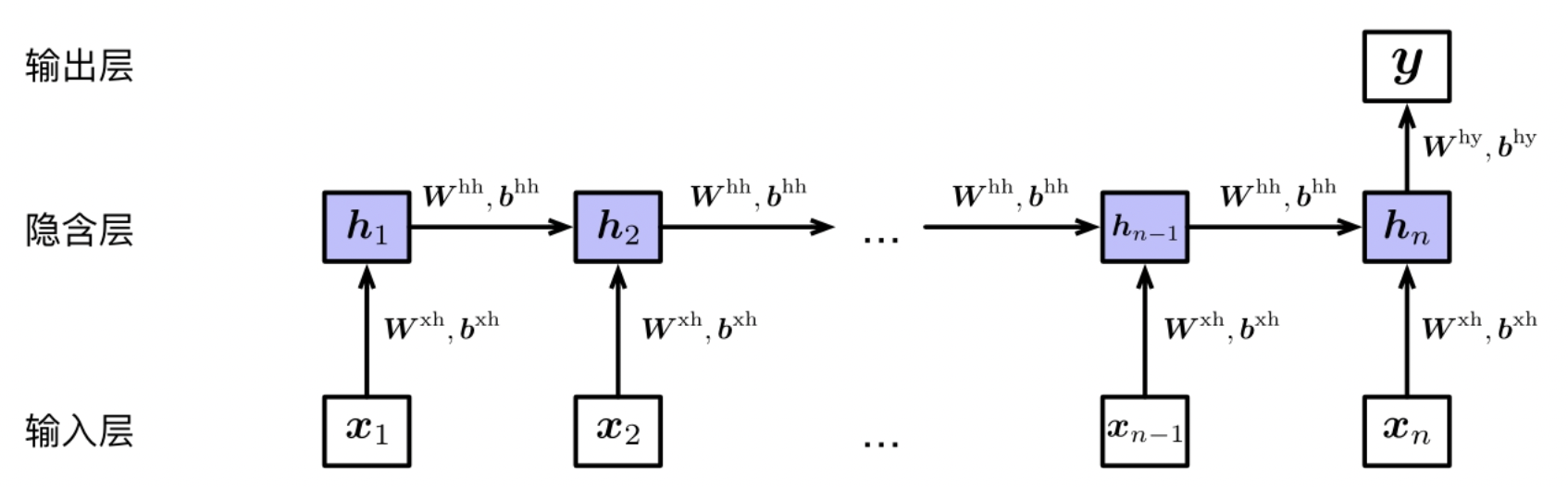
Formulaly,

$$ \begin{matrix} h_t = tanh(W^{xh}x_t + b^{xh} + W^{hh}h_{t-1} + b^{hh}) \\ y = Softmax(W^{hy}h_n + b^{hy}) \end{matrix} $$

where $tanh(z) = \frac{e^z - e^{-z}}{e^{z} + e^{-z}}$ is the activation function. The codomain of tanh is (-1, 1).
Every time, the hidden layer $h_t$ beared all input information of 1~t. So the hidden layer in the RNN alse be called Memory Unit.

LSTM Structure

The defects of RNN:

• Intuitivly, Information can be lost in the way from input to output through many hidden layers.
• The parameter might hardly be optimized because of Gradient Vanish and Gradient Explode.

Long Short Term Memory Network is a variant Recurrent Neural Network which can keep long-term memory.

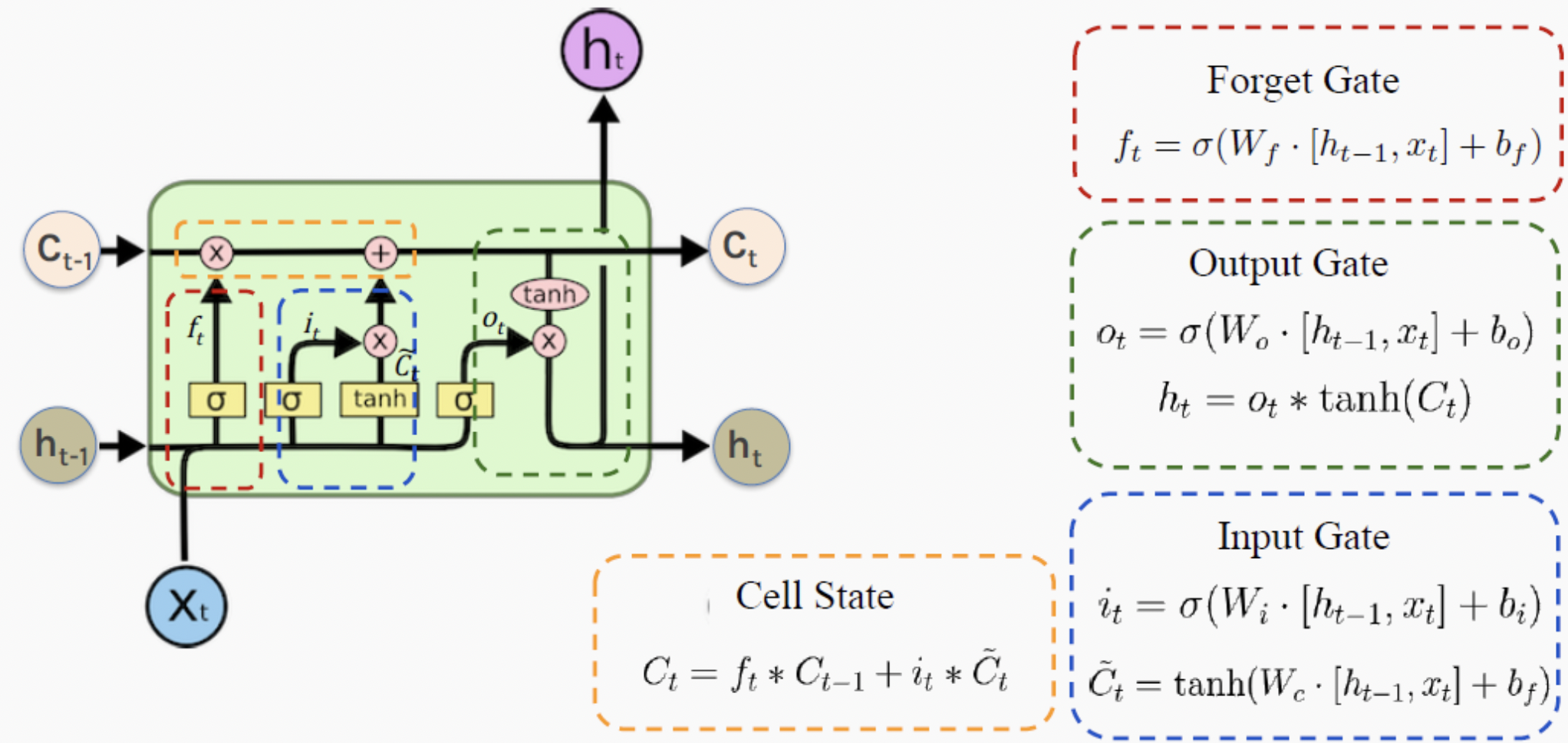
Motivation and Evolution

When we firstly see the structure figure, we might be confused of Why. Then we will derive it step by step.

(1)

$$ \begin{matrix} u_t = tanh(W^{xh}x_t + b^{xh} + W^{hh}h_{t-1} + b^{hh}) \\ h_t = h_{t-1} + u_t \end{matrix} $$

The advantage of this variant is connect $h_k$ and $h_t$ directly (k < t), striding over several layers between them. Because $h_t = h_{t-1} + u_t = h_{t-2} + u_{t-1} + u_{t} = h_k + u_{k+1} + u_{k+2} + \cdots + u_{t-1} + u_{t}$.

(2)
Simply Adding old state $h_{t-1}$ and new state $u_t$ is a rough way without considering the contribution of each state. So we add a weight as a coefficient, also called gate.

$$ \begin{matrix} f_t = \sigma(W^{f,xh}x_t + b^{f,xh} + W^{f,hh}h_{t-1} + b^{f,hh}) \\ i_t = \sigma(W^{i,xh}x_t + b^{i,xh} + W^{i,hh}h_{t-1} + b^{i,hh}) \\ h_t = f_t \odot h_{t-1} + i_t \odot u_t \end{matrix} $$

• $f_t$: Forget Gate. Smaller it is, the more old information lost.
• $i_t$: Input Date. Greater it is, the more important new information is.

(3)
We can also add Output Gate. And this is the standard LSTM.

$$ \begin{matrix} f_t = \sigma(W^{f,xh}x_t + b^{f,xh} + W^{f,hh}h_{t-1} + b^{f,hh}) \\ i_t = \sigma(W^{i,xh}x_t + b^{i,xh} + W^{i,hh}h_{t-1} + b^{i,hh}) \\ c_t = f_t \odot h_{t-1} + i_t \odot u_t \\ o_t = \sigma(W^{o,xh}x_t + b^{o,xh} + W^{o,hh}h_{t-1} + b^{o,hh}) \\ h_t = o_t \odot tanh(c_t) \end{matrix} $$

$c_t$ is named Memory Cell.

Bi-RNN

Bi means Bidirectional.

In the traditional RNN, the flow of information is sole-direciton flow. It is not suitable in some tasks. For example, Part-Of-Speech Tagging, a word is not only related to previous world, but also related to next word. But in the sole-direction structure, it can not see the next word.

To solve the problem, someone proposed Bi-RNN. The core idea is input the same input sequence into 2 RNN networks, respectively forward and backward. Then concating those hidden layers as figure shows. Finally the concat units jointly predict the output.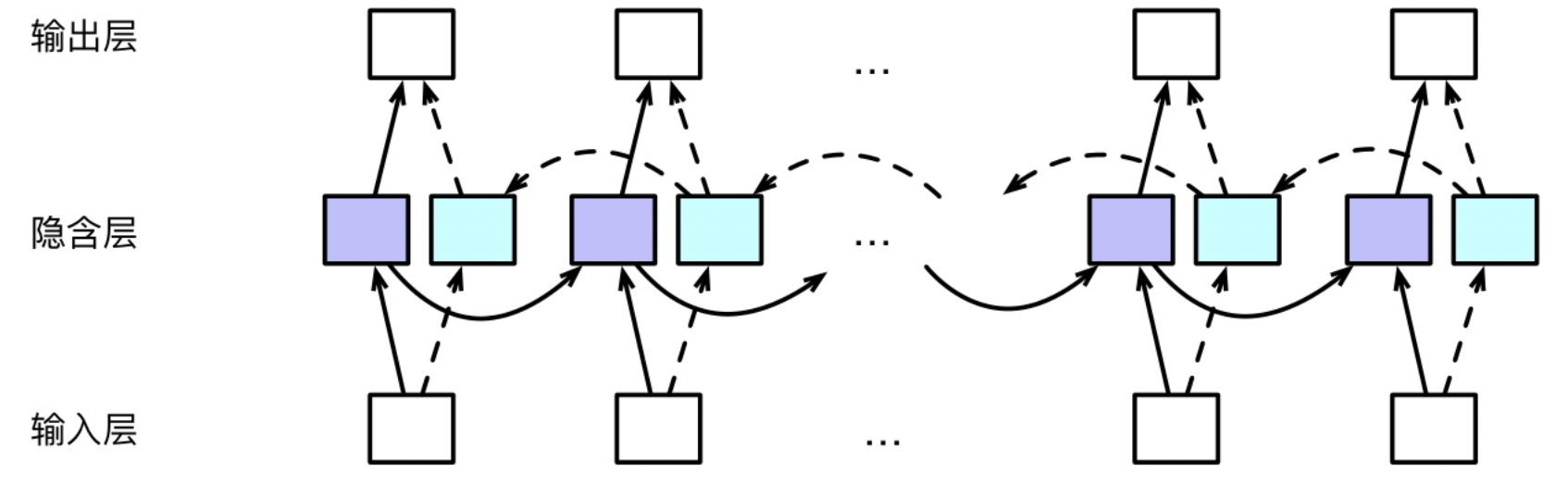

Stacked RNN

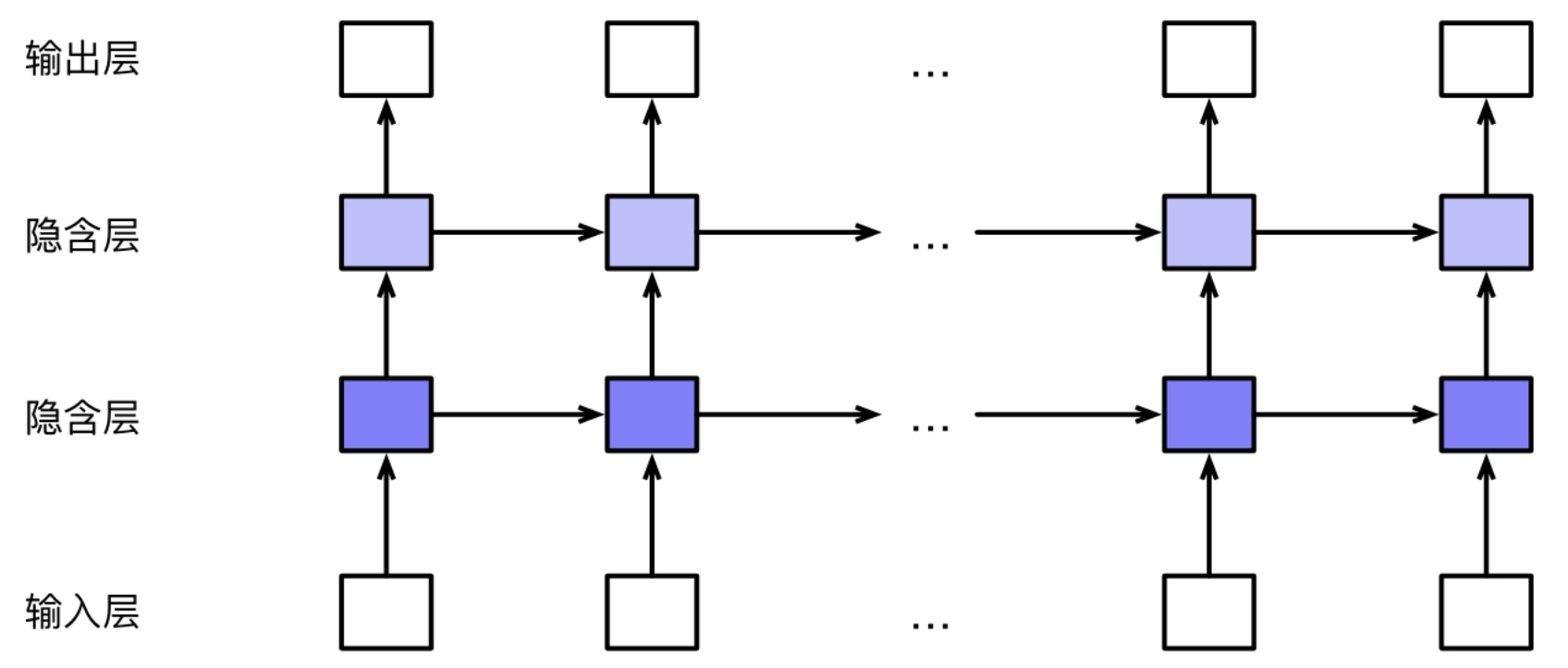
Code

RNN

from torch.nn import RNN
rnn = RNN(input_size=4, hidden_size=5, batch_first=True)

# inputs size = [batch_size, seq_len, word vector dimension]
inputs = torch.rand(2, 3, 4)

# outputs size = [batch_size, seq_len, hidden_size]
# hn size = [1, batch_size, hidden_size] : choose the last time hidden layer
outputs, hn = rnn(inputs)

Other parameters:

• bidirectional=True: Bi-RNN, default value is False.
• num_layers=2: Stacked-RNN, default values is 1.

LSTM

from torch.nn import LSTM
lstm = LSTM(input_size=4, hidden_size=5, batch_first=True)

# inputs size = [batch_size, seq_len, word vector dimension]
inputs = torch.rand(2, 3, 4)

# outputs size = [batch_size, seq_len, hidden_size]
# hn size = [1, batch_size, hidden_size] : choose the last time hidden layer
# cn size = [1, batch_size, hidden_size] : choose the last time memory cell
outputs, (hn, cn) = lstm(inputs)