^ _ ^

最短路问题

最短路问题（short-path problem）是网络理论解决的典型问题之一。基本内容是：若网络中的每条边都有一个数值（长度、成本、时间等），则找出两节点（通常是源节点和阱节点）之间总权和最小的路径就是最短路问题。

最短路问题可分为单源最短路、全局最短路和两点最短路径三种。单源最短路指确定起点或终点的最短路径求解；全局最短路求解图中所有点之间的最短路径；两点最短路径指确定起点和终点，求两节点之间的最短路径。

最短路问题中比较常用的算法有：

Dijkstra算法：时间复杂度为$O(V^2)$，可用堆进行优化，优化后时间复杂度可降为$O(E + VlogV)$，其中$E$为边数，$V$为结点数。该算法适用于求解单源最短路问题。但它只能适用于无负权边的图。
Bellman-Ford算法：时间复杂度为$O(VE)$。
SPFA算法：Bellman-Ford算法浪费了许多时间做无必要的松弛，可用SPFA算法进行优化。SPFA算法基于队列进行优化，优化后时间复杂度为$O(kE)$，其中$k$为所有顶点进队的平均次数，可以证明$k$一般小于等于2，由此可见该优化的效果十分显著。
Floyd-Warshall算法：适用于求解全局最短路问题，时间复杂度为$V^3$。该算法可以计算包含负权边的图，但不可含有负环。
搜索算法：常用的广度优先搜索（BFS）和深度优先搜索（DFS）可用于解决两点最短路径问题，时间复杂度为$O(V)$。

图结构

图算法中图的基本表示方法包括邻接表和邻接矩阵两种。这两种表示法既可用于有向图，也可用于无向图。

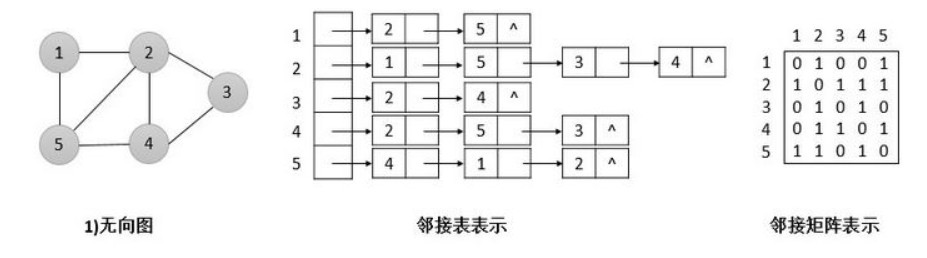
对于稀疏图（图中边数远小于点个数），用邻接表表示能更多的节省空间；而对于需要判断两个顶点之间边的情况，用邻接矩阵表示能有更快的访问速度。