^_^
单变量线性回归
模型表示
以房价预测为例,我们拥有一个数据集,数据集包含一系列住房的面积和对应的房价。这个数据集被称为训练集(Traning Set)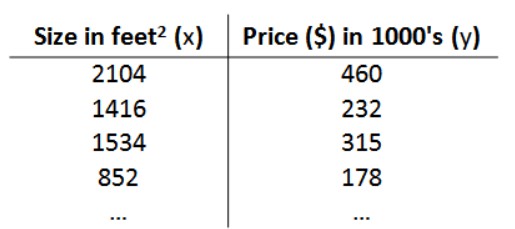
我们将要用来描述这个回归问题的标记如下:
- $m$代表训练集中实例的数量;
- $x$代表特征/输入变量;
- $y$代表目标变量/输出变量;
- $(x,y)$代表训练集中的实例;
- $(x^{(i)},y^{i})$代表第 i 个观察实例。
- $h$代表学习算法的解决方案或函数也称为假设(hypothesis)
在预测房价的例子中,$h$表示一个函数,输入是房屋尺寸大小,输出是估计房屋价格。$h$是一个从房屋大小到房屋售价的映射。要解决房价预测问题,我们实际上是要将训练集“喂”给我们的学习算法,进而学习得到一个假设,然后将我们要预测的房屋的尺寸作为输入变量输入给$h$,预测出该房屋的交易价格作为输出变量输出为结果。
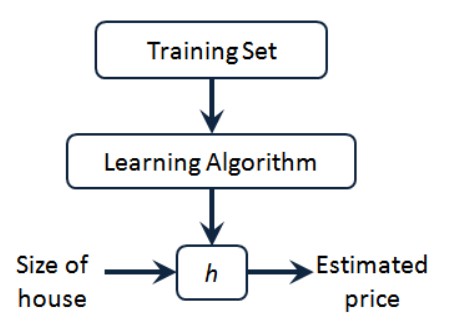
一种可能的表达方式为:$h_\theta(x) = \theta_0 + \theta_1x$,因为只含有一个特征/输入变量,因此这样的问题叫作单变量线性回归问题。
代价函数
现在要做的便是为我们的模型选择合适的参数(parameters)$\theta_0$和$\theta_1$。我们选择的参数决定了我们得到的预测相对于我们的训练集的准确程度,模型所预测的值与训练集中实际值之间的差距就是建模误差(modeling error)。
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。即使得代价函数$J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$最小。
梯度下降
梯度下降是一个用来求函数最小值的算法,我们将使用梯度下降算法来求出代价函数$J(\theta_0,\theta_1)$的最小值。
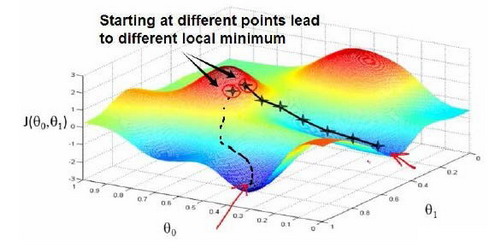
想象一下你正站立在山的这一点上,站立在你想象的公园这座红色山上,在梯度下降算法中,我们要做的就是旋转360度,看看我们的周围,并问自己要在某个方向上,用小碎步尽快下山。这些小碎步需要朝什么方向?如果我们站在山坡上的这一点,你看一下周围,你会发现最佳的下山方向,你再看看周围,然后再一次想想,我应该从什么方向迈着小碎步下山?然后你按照自己的判断又迈出一步,重复上面的步骤,从这个新的点,你环顾四周,并决定从什么方向将会最快下山,然后又迈进了一小步,并依此类推,直到你接近局部最低点的位置。
批量梯度下降(batch gradient descent)算法的公式为: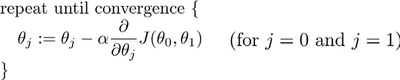
其中$\alpha$是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。
注意,所有的$\theta_i$需要进行同步更新,所以这个更新过程应该是这样的:
关于$\alpha$的选取:
- 如果$\alpha$太小的话,可能会很慢,因为它会一点点挪动,它会需要很多步才能到达全局最低点。
- 如果$\alpha$太大的话,那么梯度下降法可能会越过最低点,甚至可能无法收敛。
- 在梯度下降法中,当我们接近局部最低点时,梯度下降法会自动采取更小的幅度,这是因为当我们接近局部最低点时,很显然在局部最低时导数等于零,所以当我们接近局部最低时,导数值会自动变得越来越小,所以梯度下降将自动采取较小的幅度,这就是梯度下降的做法。所以实际上没有必要再另外减小$\alpha$。
这就是梯度下降算法,你可以用它来最小化任何代价函数$J$,不只是线性回归中的代价函数$J$。
梯度下降的线性回归
我们要将梯度下降应用于具体的拟合直线的线性回归算法里。
梯度下降算法和线性回归算法比较如图:
对我们之前的线性回归问题运用梯度下降法,关键在于求出代价函数的导数,即: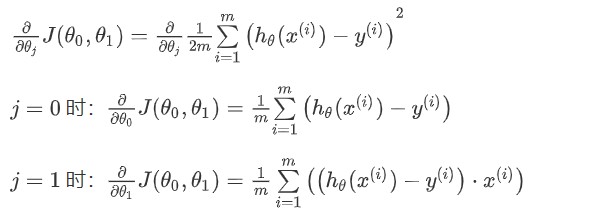
则算法改写成: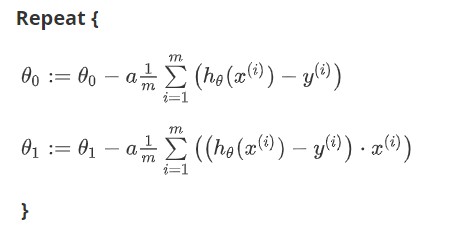
我们刚刚使用的算法,有时也称为批量梯度下降。实际上,在机器学习中,通常不太会给算法起名字,但这个名字”批量梯度下降”,指的是在梯度下降的每一步中,我们都用到了所有的训练样本。
多变量线性回归
多变量回归模型
目前为止,我们探讨了单变量/特征的回归模型。以房价预测为例。现在我们对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为$(x_1,x_2,\cdots,x_n)$。
增添更多特征后,我们引入一系列新的注释:
- $n$代表特征的数量;
- $x_j^{(i)}$代表特征矩阵中第$i$行的第$j$个特征,也就是第$i$个训练实例的第$j$个特征;
- 支持多变量的假设$h$表示为:$h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \cdots + \theta_nx_n$,这个公式中包含$n+1$个参数和$n$个变量,为了简化公式,引入$x_0=1$,则公式转换为$h_\theta(x) = \theta_0x_0 + \theta_1x_1 + \theta_2x_2 + \cdots + \theta_nx_n$;
- 特征矩阵$X$的维度是$m \times (n+1)$, 因此公式可以简化为:$h_\theta(x) = \theta^TX$
多变量梯度下降
与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和,即:$J(\theta_0,\theta_1,\cdots,\theta_n)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$
我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。 多变量线性回归的批量梯度下降算法为: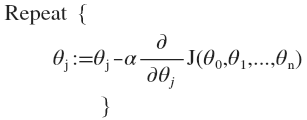
求导数后得到: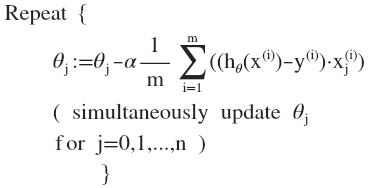
特征缩放
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000平方英尺,而房间数量的值则是0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。
解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间。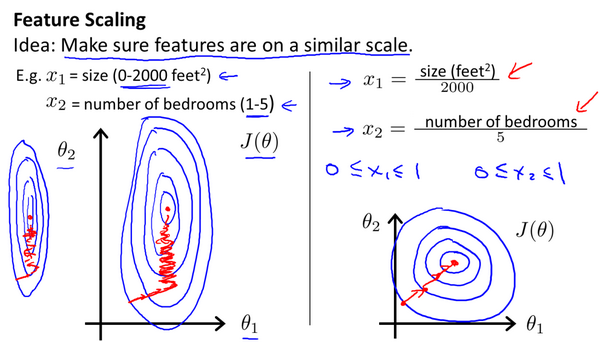
最简单的方法是令:$x_n = \frac{x_n-\mu_n}{s_n}$,$\mu_n$是平均值,$s_n$是标准差。
学习率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。
也有一些自动测试是否收敛的方法,例如将代价函数的变化值与某个阀值(例如0.001)进行比较,但通常绘制图表更好。
通常可以考虑尝试些学习率:$\alpha = 0.01,0.03,0.1,0.3,1,3,10$
特征和多项式回归
线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如一个二次方模型或者三次方模型,通常我们需要先观察数据然后再决定准备尝试怎样的模型。 另外,我们可以令某变量的n次方用另一个1次变量进行替代,从而将模型转化为线性回归模型。
注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。
正规方程
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的:$\frac{\partial}{\partial \theta_j}J(\partial_j) = 0$。假设我们的训练集特征矩阵为$X$(包含了$x_0=1$),并且我们的训练集结果为向量$y$,则利用正规方程解出向量$\theta = (X^TX)^{-1}X^Ty$
如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为$O(n^3)$,通常来说当n小于10000 时还是可以接受的。正规方程法只适用于线性模型,不适合逻辑回归模型等其他模型。